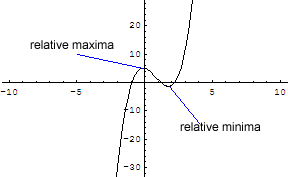
Relative Maxima and Minima
Relative maxima and minima are basically the high and low points on the graph of a function.
 |
These points, also referred to as critical points can be found by the First
Derivative Test.
If f'(x) > 0, and x < c, and f'(x) < 0 for x > c, then f(c) is a
relative maximum.
If f'(x) < 0, and x < c, and f'(x) > 0 for x > c, then f(c) is a
relative minima.
If the sign of f'(x) doesn't change at x = c, then there is no relative max
or min there.
Find the relative extrema of f(x) = 1/3x^3+7/2x^2+12x+9.
The derivative is x^2+7x+12.
This factors into (x+4)(x+3), thus giving us the critical numbers -4, and -3.
Make a sign graph and determine the sign for the intervals (-inf,-4), (-4,-3),
(-3,+inf).
+ for (-inf,-4)
- for (-4,-3)
+ for (-3,+inf)
We make the conclusion that f(-4) = -9/2 is a relative maximum, and that f(-3)
= -13/3 is a relative minimum.
Make sure you understand that there is no relative max/min if the derivative's
sign does not change at a critical number.
An example is f(x) = x^3.
The derivative is f'(x) = 3x^2, critical number is 0. The function is ALWAYS
increasing, thus it has no relative extrema.