Product and Quotient Rule

Alright. You know how to find the derivative of something like f(x) = x^2+5x+6, (that is I hope you know how by now..)but what if you had it in this form: p(x) = (x+3)(x+2)? Though they're the same thing, there's another approach you can take.

The Product rule. f*g = gf' + g'f.

Cool, so do exactly as it says. Let f be x+3, and let g be x+2.
p'(x) = (x+2) * (x+3)' + (x+3) * (x+2)'
p'(x) = (x+2) * (1) + (x+3) * (1)
p'(x) = x+2 + x+3
p'(x) = 2x+5.

Althought it seems like more work, it makes things easier if you have a monster function like f(x) = (x^5+x^4+x^3+x^2)(x^5+x+1) and want to find f'(x). You probably don' t want to expand that..

Here's some more exercises, practice makes perfect.
1. q(x) = (x^2+3)(x^3+2x), find q'(x).

2. u(x) = (x^3+x^2+x)(x^3-1), find u''(x)

3. a(x) = (x^5+4x)(x^2+2x+1), find a'(x)

Now that we know how to work with finding the derivative of the product of two polynomials, what about the derivative of the quotient of two polynomials?

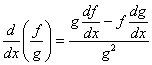The quotient rule. f/g = (gf' -g'f)/g^2.

So, lets see it in action.
p(x) = (5x^2+x)/(x), find p'(x)
let f = (5x^2+x), let g = (x).
p'(x) = ((x) * (5x^2+x)' - (5x^2+x) * (x)')/(x)^2
p'(x) = ((x) * (10x+1) - (5x^2+x) * (1))/(x)^2
p'(x) = ((10x^2+x - 5x^2+x))/x^2
p'(x) = (5x^2+2x)/x^2

This is useful because in most cases even doing the division by long-division will yield a remainder polynomial that you'll still have to operate on with this rule.

Here are some very fun examples.
1. c(x) = (5x^2+x+1)/(x^10+x), find c'(x)

2. k(x) = (25x^3+2x)/(x^3-1), find k'(x)